TRZECI WYMIAR
Szczytowym osiągnięciem malarza jest dokonać tego, aby powierzchnia płaska ukazała ciała wypukłe i występujące z owej płaszczyzny (Leonardo da Vinci, 1792/2006)
Żyjemy w przestrzeni wyznaczonej przez trzy wymiary: horyzontalny (w prawo lub w lewo), wertykalny (w górę lub w dół) i w głąb (z przodu lub z tyłu). W tak rozumianej przestrzeni widzimy obiekty i możemy stosunkowo trafnie określić ich położenie na każdym z tych wymiarów. Oczywiście jest tak pod warunkiem, że, po pierwsze dysponujemy sprawnie działającym systemem wzrokowym na całej długości od siatkówek obu oczu do korowego szlaku grzbietowego, po drugie, zajmujemy centralną (egocentryczną) pozycję w tej przestrzeni oraz po trzecie, jesteśmy wystarczająco doświadczeni w poruszaniu się w tej przestrzeni (Milner i Goodale, 2008).
Wymiar horyzontalny i wertykalny wyznaczają płaszczyznę prostopadłą do osi widzenia, a wymiar w głąb wyznacza linię równoległą do niej. Widzenie sceny w trzech wymiarach oznacza zatem widzenie zbioru płaszczyzn prostopadłych do osi widzenia, które znajdują się w różnej odległości od nas, na osiach wzdłuż trzeciego wymiaru. Minimalnym warunkiem widzenia obiektu w przestrzeni jest zatem dostrzeżenie którejkolwiek z jego powierzchni w taki sposób, że jej izometryczny rzut na płaszczyznę prostopadłą do osi widzenia, można opisać za pomocą niezerowych wartości na wymiarze horyzontalnym i wertykalnym. Nie widzimy w scenie tych rzeczy, których izometryczne rzuty na płaszczyznę prostopadłą do osi widzenia przyjmują wartości zerowe na którymkolwiek z tych dwóch wymiarów.
Nieco bardziej skomplikowana jest sytuacja z widzeniem w głąb. Jak wszystko, w co wyposażyła nas ewolucja, również mechanizmy widzenia w głąb są przede wszystkim podporządkowane zachowaniu bezpieczeństwa, czyli przeżyciu. W naturalnych warunkach szczególną uwagą systemu wzrokowego jest objęty obszar do ok. 6 m wokół nas. Wtargniecie kogoś lub czegoś w tę przestrzeń wymaga precyzyjnych reakcji, np. obrony i nie może tutaj być miejsca na jakieś błędy w ocenie odległości tego kogoś lub czegoś od nas.
W jeszcze mniejszym obszarze wokół nas, czyli w przestrzeni wyznaczonej zasięgiem rąk jeszcze bardziej konieczna jest wysoka precyzja w ocenie odległości rzeczy lub ich fragmentów od nas. Prawdopodobnie, dzięki rozwinięciu umiejętności precyzyjnego operowania przedmiotami w niewielkiej odległości od oczu możliwe stało się wytwarzanie precyzyjnych narzędzi, a także rzeźb. Być może rzeźbienie pierwszych Wenus w jaskini Hohle Fels, 35–40 tys. lat temu było tylko odpryskiem wojowniczo nastawionej natury naszych przodków na rozwój nowoczesnych technologii zabijania, ale jakże zbawienne dla rozwoju kultury duchowej człowieka. Tak czy inaczej, w odniesieniu do najbliższej przestrzeni wokół nas działa kilka neuropoznawczych mechanizmów kontrolujących obecność rzeczy znajdujących się w głębi oglądanych scen. Najważniejsze z nich są związane z dwuocznością.
Świadomość uporządkowania rzeczy wzdłuż trzeciego wymiaru w krótszym dystansie, czyli mniej więcej do granicy 6 m, jest przede wszystkim wynikiem widzenia stereoskopowego (binocular vision), a w szczególności tzw. rozbieżności dwuocznej (binocular disparity) oraz odruchów wergencyjnych oczu (vergence). Doświadczenie widzenia przestrzenności sceny wizualnej powstaje w wyniku działania neurofizjologicznych mechanizmów przetwarzania danych dotyczących reakcji fotoreceptorów wzbudzonych przez dwuwymiarowe obrazy rzutowane na siatkówki obu oczu obserwatora. Jeśli między rzutami tych obrazów na odpowiadające sobie przestrzennie pola recepcyjne obu siatkówek oczu występują różnice w zakresie reakcji fotoreceptorów, wówczas na korowych etapach szlaku wzrokowego, dane te są integrowane w jeden obraz, zawierający informację o uporządkowaniu widzianych płaszczyzn w głąb.
Nietrudno się domyślić, że pierwsze sygnały dotyczące rozbieżności dwuocznej są przedmiotem analiz w korze V1, w której w ramach jednej struktury anatomicznej porządkowane są dane pochodzące z prawego i z lewego oka. Badania na ten temat były prowadzone już kilka lat po odkryciach Hubela i Wiesela dotyczących budowy kory V1, m.in. przez Horace B. Barlowa, Colina Blakemore i Jacka Pettigrewa (1967). Dalsze analizy w zakresie rozbieżności dwuocznej prowadzone są w strukturach płatów ciemieniowych na szlaku grzbietowym, a zwłaszcza w obszarze V5.
Jeżeli rozbieżność dwuoczna jest zbyt duża, tzn. jeżeli obrazy rzutowane na siatkówki obu oczu obserwatora są całkowicie inne, wówczas dochodzi do tzw. rywalizacji dwuocznej (binocular rivalry). W takiej sytuacji różnice między obrazami nie są interpretowane jako wskaźnik głębi, tylko jeden z tych obrazów, najczęściej rzutowany na siatkówkę dominującego oka, jest traktowany jako właściwy, a drugi ignorowany.
Druga grupa mechanizmów związanych z widzeniem stereoskopowym dotyczy odruchów wergencyjnych, czyli konwergencji (convergence) i dywergencji (divergence) gałek ocznych. To zagadnienie zostało już omówione w rozdziale dotyczącym kadrowania sceny wizualnej. Zbieżny (konwergencyjny) ruch oczu jest przejawem większego zainteresowania obiektami położonymi bliżej obserwatora, natomiast ruch rozbieżny (dywergencyjny), wskazuje na zainteresowanie obiektami oddalonymi nieco od obserwatora, ale tylko do granicy ok. 6 m, ponieważ powyżej tej odległości linie pola widzenia są niemal równoległe do siebie.
Ponieważ w tej książce koncentruję się na oglądaniu płaskich obrazów, dlatego dwuoczne wskaźniki głębi(binocular cues of depth perception), czyli rozbieżność dwuoczna i odruchy wergencyjne nie będą już szerzej omawiane. Z punktu widzenia podejmowanej tutaj problematyki znacznie bardziej interesujące są te mechanizmy widzenia głębi, które nie wymagają dwuoczności. Są one znacznie bardziej uniwersalne, ponieważ nie tylko pozwalają na ocenę porządku rzeczy w głąb w scenie trójwymiarowej, niezależnie od tego czy znajdują się one blisko czy daleko od obserwatora, ale również stanowią podstawę iluzji trzeciego wymiaru na obrazach. Są to tzw. niestereoskopowe lub po prostu, jednooczne wskaźniki głębi.
Przestrzeń widziana okiem Cykolpa
Jednooczne wskaźniki głębi (monocular depth cues) stanowią podstawę rozumienia relacji przestrzennych w głąb między obiektami przedstawionymi na płaskim obrazie lub w przestrzeni trójwymiarowej, praktycznie niezależnie od odległości od obserwatora. Trafność interpretacji tych wskaźników jest wynikiem procesu uczenia się, w jaki sposób określone wzorce płaszczyzn, ich konturów i barw oraz ich zmienność w ruchu reprezentują rzeczywiste relacje w przestrzeni trójwymiarowej. Hipotezę tę wspierają wyniki badań międzykulturowych, w których materiałem bodźcowym były ilustracje (obrazy, rysunki, zdjęcia) przedstawiające sceny zawierające nieznane w innych kulturach wskaźniki głębi (np. Duncan, Gourlay i Hudson, 1973; Gibson, 1988; Hudson, 1960; Jahoda, Deregowski, Ampene i Williams, 1977; Jahoda i McGurk, 1974; Liddell, 1996; 1997; Serpell i Deregowski, 1980).
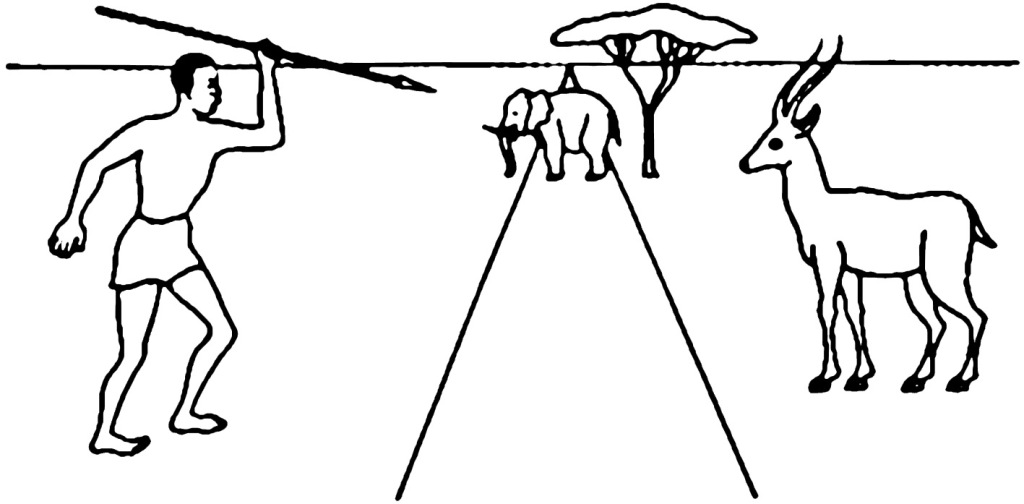
Robert Serpell i Jan B. Deregowski (1980) dowodzą, że wprowadzenie do przedstawienia sceny polowania wskaźników głębi, tak jednoznacznie oczywistych dla osób z kręgu kultury zachodnioeuropejskiej, jak linia horyzontu, zbiegające się krawędzi drogi oraz właściwe proporcje w wielkości przedstawionych obiektów w pierwszym i w drugim planie (ryc. 134), bynajmniej nie stanowią żadnej wartościowej wskazówki dotyczącej przestrzeni, dla rdzennych mieszkańców Ghany, Zambii czy Ugandy. Afrykanie niezmiennie interpretowali tę scenę, jako polowanie na słonia, a nie na antylopę.
Widzenie głębi przedstawionej na płaskim obrazie w oparciu o jej jednooczne wskaźniki jest wynikiem aktywności neurofizjologicznych mechanizmów rozwijających się na podobnych zasadach jak działa, np. mechanizm umożliwiający oddzielnie obiektu od jego cienia. W odniesieniu do obiektów nowych możemy się łatwo pomylić, przyjmując za jego część to, co faktycznie jest jego cieniem. W wyniku licznych doświadczeń przekonujemy się, że zarówno kontur, jak i barwa obiektu wizualnego i jego cienia mają nieco inne własności. Ich dostrzeżenie, sklasyfikowanie i zapamiętanie stanowią podstawę trafnego rozpoznawania rzeczy w przyszłości, zarówno w trójwymiarowym świecie, jak i na obrazach.
Podobnie jest z percepcją głębi. Z doświadczenia wiemy, że np. wielkości tych samych rzeczy w scenie wizualnej najczęściej są uzależnione od ich odległości od obserwatora. I chociaż z pewnością ta obserwacja jest dana ludzkości niemal od zarania dziejów, to trzeba było ponad 30 tys. lat (licząc od powstania naskalnych malowideł w Lascaux, Altamirze i Chauvet), aby zasady perspektywy linearnej zaczęły być świadomie wykorzystywane przez artystów w Zachodniej kulturze do przedstawiania trójwymiarowych scen wizualnych na płaskich obrazach (Alberti, 1963; Janowski, 1997). Dopiero na początku XV wieku Filippo Brunelleschi skodyfikował zasady perspektywy linearnej i za pośrednictwem wielowiekowego przekazu kulturowego zostały one włączone do kanonu podstawowych jednoocznych wskaźników głębi. Nabycie umiejętności korzystania z tego wskaźnika wymagało czasu i treningu, czyli po prostu nauczenia się, w jaki sposób ujawnia on przestrzenność przedstawionej sceny wizualnej w trzecim wymiarze.
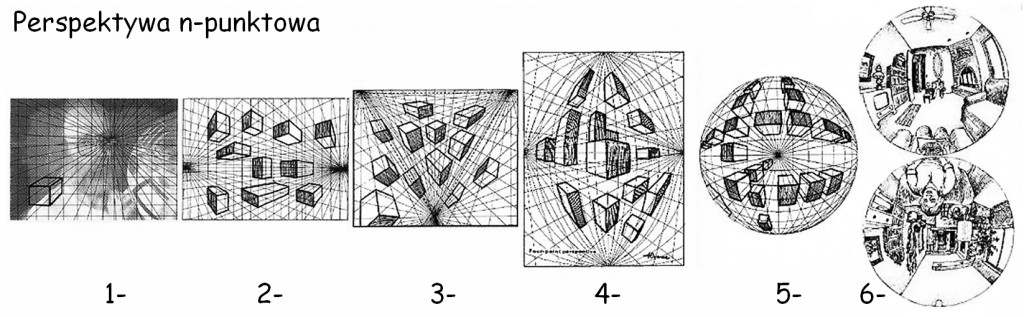
Chociaż renesansowe rozwiązanie Brunelleschiego wydaje się najbardziej oczywistą formą przedstawiania na obrazie przestrzeni trójwymiarowej, tym niemniej z całą pewnością nie jest to jedyna, akceptowana przez ludzki umysł perspektywa. Dowodzą tego bardzo interesujące propozycje graficzne i malarskie Dicka Termesa, który jest zafascynowany, nie jedno- czy dwupunktową perspektywą widzenia rzeczy, ale sześciopunktową perspektywą sferyczną (ryc. 135). Zarówno jego eksperymenty, jak i studia nad sposobami obrazowania przestrzeni w przeszłości dowodzą, że nie mamy dobrej odpowiedzi na pytanie, w jaki sposób przebiegają linie perspektywy podczas widzenia trójwymiarowych scen. Nie potrafimy nawet zgodzić się co do tego, czy te linie są proste czy krzywe. Czerpiąc wiedzę z optyki łatwiej jest nam myśleć o prostoliniowych osiach widzenia i równoległych do nich liniach zbiegu perspektywy, niż liniach biegnących wzdłuż krawędzi kuli.
Obecnie znamy już wiele jednoocznych wskaźników głębi, które stanowią podstawę widzenia trzeciego wymiaru na płaskich obrazach. Funkcjonalność wszystkich tych wskaźników jest weryfikowana poprzez niezliczone codzienne doświadczenia wizualne i ruchowe. Patrząc na płaski obraz przedstawiający przestrzeń trójwymiarową wykorzystujemy je automatycznie. Stwarzają one niekwestionowaną iluzję trójwymiarowości obrazu i dopiero złamanie przez artystę zasady leżącej u podłoża któregoś z tych wskaźników zmusza nas do rewizji przekonania o przestrzenności tego, co właśnie oglądamy. Znakomitych przykładów potwierdzających to przypuszczenie dostarczają iluzoryczne przestrzenie Mauritsa Cornelisa Eschera (ryc. 136).

Do pierwszej grupy jednoocznych wskaźników głębi należą te, które definiują głębię na podstawie relacji między elementami w przedstawionej na obrazie scenie wizualnej lub w odniesieniu do jego ram. Są to: interpozycja lub inaczej okluzja (occlusion), czyli zasłanianie jednych obiektów przez inne, transpozycja (elevation), określająca zależność między położeniem rzeczy na obrazie względem linii horyzontu a ich iluzoryczną odległością od obserwatora oraz perspektywa liniowa (linear perspective) i krzywoliniowa (curvelinear perspective), zero‑, jedno- lub wielopunktowa.
Druga grupa wskaźników opiera się na zacieraniu konturów widzianych rzeczy w wyniku zagęszczania gradientu struktury powierzchni (texture gradient) lub ostrości (wyrazistości) widzenia detali (sharpness of details). Podstawowa reguła interpretacyjna tych wskaźników brzmi: im mniej różnicowalna jest powierzchnia rzeczy przedstawionych na obrazie, tym większa jest ich odległość od obserwatora w głąb sceny wizualnej.
Wreszcie trzecią grupę wskaźników głębi łączy związek z luminancją i barwą przedstawianych rzeczy. Do najważniejszych wskaźników w tej grupie należy: światłocień (chiaroscuro), perspektywa powietrzna (aerial perspective) i separacja barw (color separation). Rozkład światła i intensywności zacienienia płaszczyzn rzeczy i przestrzeni wokół nich zasadniczo jest interpretowany zgodnie z następującą zasadą: im jaśniej tym bliżej, a im ciemniej tym bardziej w głąb. Nie bez znaczenia dla interpretacji światłocienia jako wskaźnika głębi jest także założenie dotyczące położenia światła względem obiektu, bez którego nie rzuca on przecież cienia.
Oglądając odległe rzeczy, np. góry na horyzoncie, na ogół widzimy je znacznie mniej wyraźnie niż obiekty bliskie, ale przede wszystkim, widzimy je jakby za błękitno-szarą mgiełką. To właśnie gęstość tej mgiełki definiuje perspektywę powietrzną. Ostatni ze wskaźników, czyli separacja barw, jest najbardziej kontrowersyjny. Zdaniem, np. Pabla Picassa barwy w ogóle nie biorą udziału w kodowaniu przestrzeni. Mają wyłącznie charakter symboliczny. Z kolei według, np. Paula Cézanne’a lub XVII-wiecznych akademików jest przeciwnie, barwy ciepłe są bliżej obserwatora, a zimne – dalej.
Spośród wymienionych wskaźników głębi najbardziej oczywistym a zarazem budzącym najmniej kontrowersji jest inkluzja. Możemy mieć wątpliwości czy artysta poprawnie odzwierciedlił perspektywę obrazowanej przestrzeni, czy zgodnie z konwencją posłużył się takimi czy innymi barwami dla podkreślenia głębi, ale co do jednego nie mamy wątpliwości: obiekt zasłaniany nie może znajdować się bliżej nas niż zasłaniający go. Wyniki badań międzykulturowych wskazują na to, że afrykańskie dzieci w latach 60. XX wieku miały najmniej problemów z poprawną interpretacją głębi na podstawie inkluzji przedstawionej na obrazkach testu Hudsona (1960). Z jednej strony, niemal wyłącznie oglądamy przedmioty, które są albo zasłonięte przez inne albo je zasłaniają i zawsze interpretujemy to spostrzeżenie, jako wiarygodny wskaźnik ich odległości od nas. Z drugiej jednak strony, bliższe przyjrzenie się mechanizmom odpowiedzialnym za rozumienie zależności zasłaniania ujawnia ich złożoność. Z tych oto powodów, w następnym rozdziale nieco dokładniej omówię właśnie ten wskaźnik widzenia głębi.
Tożsamość rzeczy, jako fundament widzenia wzdłuż trzeciego wymiaru
Niezależnie od wymienionych wskaźników głębi, które bardziej lub mniej poprawnie można zastosować na obrazie w celu nadania scenie trójwymiarowej plastyczności, wszystkie one mają jedną wspólną cechę: są własnościami obrazu. Innymi słowy, rysując lub malując obraz można użyć każdego z nich w celu podkreślenia przestrzenności sceny w głąb. To, w jaki sposób zostanie jednak zinterpretowany dany wskaźnik głębi nie jest już cechą obrazu tylko obserwatora, a ściślej jego zdolności do spostrzegania rzeczy jako tożsamych niezależnie od warunków percepcyjnych (Lawson, 1999).
Żaden z trzech wymiarów przestrzeni nie dzieła tak destruktywnie dla stałości widzenia rzeczy, jak wymiar w głąb. Przestrzenność wpływa nie tylko na wielkość widzianych rzeczy, ale przed wszystkim powoduje, że wciąż mamy do czynienia z innym ich wyglądem. Ta zmienność jest wynikiem zarówno przyjmowania przez obserwatora różnych punktów widzenia, jak i inkluzji, która bezlitośnie dostarcza nam zaledwie szczątków kompletnych obrazów. Zespół tych cech umysłowych, które przeciwdziałają destrukcyjnym wpływom widzenia w głąb określany jest jako zasady stałości widzenia (visual object constancy), spośród których dwie są szczególnie istotne w odniesieniu do obrazów. Są to: stałość kształtu i wielkości. Od nich rozpocznę omawianie zagadnienia widzenia głębi na płaskich obrazach.
ZASADY STAŁOŚCI WIDZENIA
Stałość kształtu
Spostrzeganie złożonych kształtów rzeczy, jako tych samych pomimo tego, że są one widziane z nowego lub nietypowego punktu, w niekorzystnych warunkach oświetleniowych, albo że są one częściowo przysłonięte, nazywa się stałością kształtu (shape constancy) (Palmer, 1999; Pizlo, 2008; Vogels i Orban, 1996). Stałość kształtu jest jednym z podstawowych czynników pozwalających na rozpoznanie przedmiotu, osoby lub relacji między nimi, niezależnie od tego czy ich obraz rzutowany na siatkówkę oka w danej chwili jest taki sam czy inny, jak rzutowany wcześniej (Pizlo, Sawada, Li, Kropatsch i in., 2010).
Poczucie stałości kształtu stanowi jeden z filarów widzenia. W szczególności odnosi się jednak do percepcji głębi ponieważ trójwymiarowość przestrzeni jest jednym z tych czynników, które znacząco wpływają na zmienność kształtów rzeczy, rozumianych jako ich izometryczne rzuty na powierzchnie siatkówek oczu. Musimy przecież pamiętać o tym, że chociaż żyjemy w świecie trójwymiarowym, w którym wymiar „w głąb” najczęściej interpretujemy, jako „z przodu” lub „przed nami”, to jednak w akcie widzenia dane o nim są sprowadzane do dwuwymiarowych obrazów siatkówkowych. Doświadczenie trzeciego wymiaru nie jest nam dane zatem bezpośrednio w taki sposób, jak np. doświadczenie widzenia światła, ale jest swego rodzaju wnioskiem wynikającym z wielu przesłanek zawartych w płaskich, siatkówkowych obrazach.
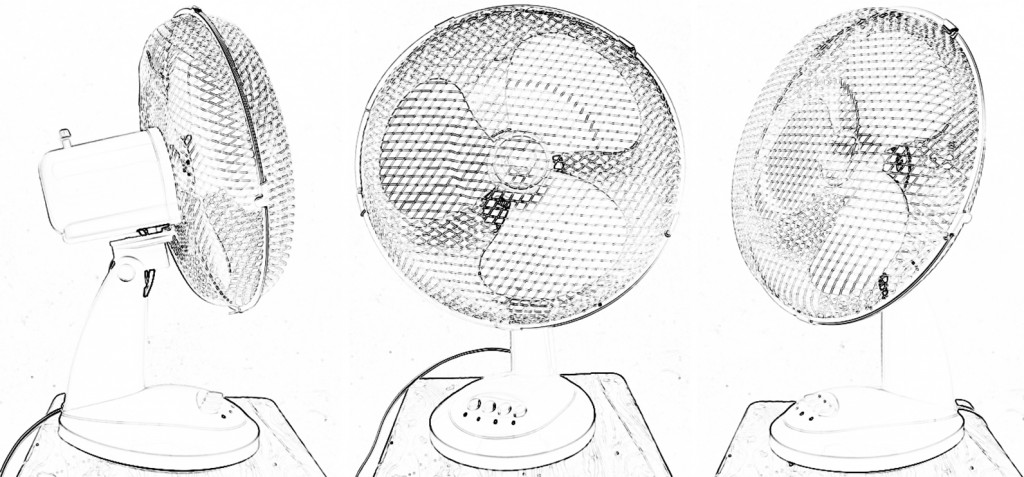
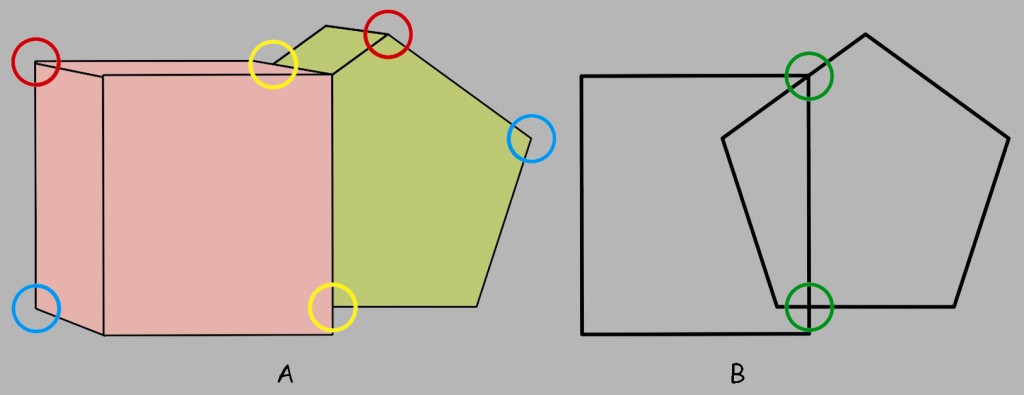
Przykładem ilustrującym stałość kształtu jest doświadczenie oglądania tego samego przedmiotu z różnych punktów widzenia (ryc. 137 A).

Jeśli spojrzymy na kontury, jakie najprawdopodobniej zostaną uchwycone na podstawie ich obrazów rzutowanych na siatkówki oczu to przekonamy się, że są one zasadniczo różne (ryc. 137 B). Nie przeszkadza nam to jednak myśleć o tym obiekcie, jako o tym samym. I na tym właśnie polega cudowne doświadczenie stałości kształtu. Doprawdy trudno sobie wyobrazić życie bez tej umiejętności chwytania istoty rzeczy pomimo zmienności jej wyglądu.
Moses W. Chan, Adam K. Stevenson, Yunfeng Li i Zygmunt Pizlo (2006) stwierdzili, że stałość kształtu obiektów trójwymiarowych jest ściśle związana z takimi ich cechami, jak: symetria (symmetry), widoczność konturów wyznaczających płaszczyzny (planar contours) oraz objętość (volume). W zachowaniu stałości kształtu szczególnie ważną rolę odgrywa symetria. Asymetryczność utrudnia rozpoznanie przedmiotu oglądanego z różnych punktów widzenia. Podobnie mniejszą stałością kształtu charakteryzują się te obiekty, w których trudno jest zidentyfikować płaszczyzny oraz są pozbawione objętości.
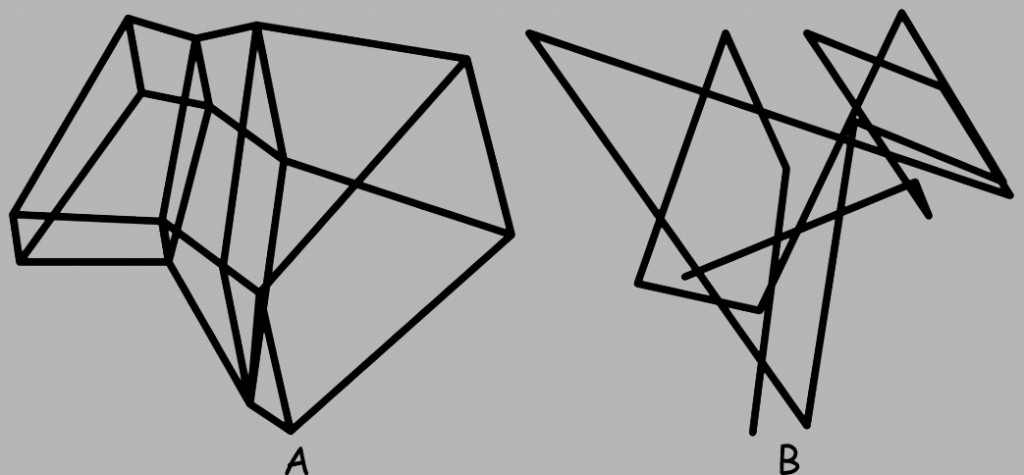
Obiekty trójwymiarowe przedstawione na ryc. 138 różnią się stałością kształtu. Co prawda obydwa są asymetryczne, ale obiekt A ma wyraźnie widoczne płaszczyzny, które połączone ze sobą sugerują jego bryłowatość, a zatem i objętość, podczas gdy obiekt B nie przypomina bryły. Zdecydowanie łatwiej byłoby nam rozpoznać obiekt A z innego punktu widzenia, niż obiekt B.
Zygmunt Pizlo, Yunfeng Li i Robert M. Steinman (2008) twierdzą, że stałość kształtu obiektów trójwymiarowych oglądanych z niewielkiego dystansu bynajmniej nie jest, ani koniecznie, ani wystarczająco związana z rejestrowaną przez mózg rozbieżnością obrazów na siatkówkach obu oczu (binocular disparity). Podstawę stałości kształtu stanowią przede wszystkim wymienione cechy tych obiektów widziane w płaszczyźnie dwuwymiarowej.
Warto w tym miejscu przywołać jeszcze jedną koncepcję, w ramach której podejmuje się zagadnienie stałości kształtu, jako zasady kategoryzacji percepcyjnej. Chodzi o ideę tzw. perspektywy kanonicznej (canonical perspective), z jakiej widziany jest obiekt. Twórcami tej koncepcją są Stephen E. Palmer, Eleanor H. Rosch i Paul Chase (1981). Pokazywali oni osobom badanym fotografie obiektów naturalnych uchwyconych z różnych punktów widzenia i prosili je o ich rozpoznanie. Okazało się, że w odniesieniu do każdego przedmiotu istnieje najbardziej preferowany punkt widzenia, z którego jest on najszybciej trafnie rozpoznawany. Z tego punktu widzenia, wygląd (kształt) obiektu ujawnia najwięcej istotnych szczegółów niezbędnych do jego rozpoznania oraz jest on najczęściej z tego punktu widziany w codziennych doświadczeniach (Blanz, Tarr i Bulthoff, 1999). Innymi słowy, kształt rzeczy uchwycony z kanonicznej perspektywy jest kształtem prototypowym, do którego umysł porównuje widziane aktualnie kształty przedmiotów, podczas ustalania ich tożsamości.
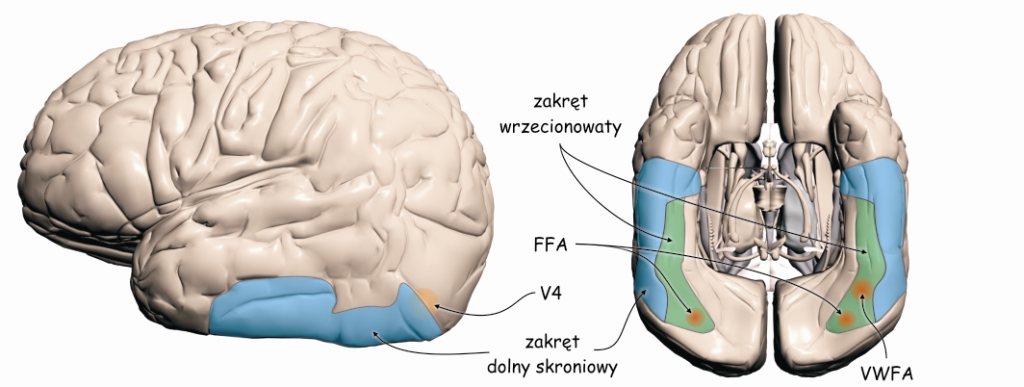
Za percepcję złożonych kształtów rzeczy jako tożsamych, czyli innymi słowy, za ich stałość odpowiedzialne są dwie struktury mózgu leżące na szlaku brzusznym, czyli zakręt dolny skroniowy (inferior temporal gyrus; IT) oraz leżący tuż nad nim od wewnętrznej strony kory – zakręt wrzecionowaty (fusiform gyrus), do których dane wzrokowe płyną głównie z pola V4 (Tanaka, 1993; 1996). Obecnie wiadomo już także, że stałość widzenia kształtów liter i słów jest również związana z aktywnością neuronów w zakręcie wrzecionowatym, ale tylko z lewej strony mózgu, w obszarze VWFA (visual word form area) (Dehaene i Cohen, 2011). Wiadomo również, że stałość widzenia kształtów twarzy, która stanowi podstawę ich rozpoznawania jest związana z aktywnością neuronów znajdujących się w obszarze zakrętu wrzecionowatego po prawej stronie mózgu lub po obu jego stronach (Farah, 1996; Feinberg, Schindler, Ochoa, Kwan i in., 1994; Kanwisher, McDermott i Chun, 1997; McCarthy, Puce, Gore i Allison, 1997; ryc. 139).

kontrast jasności, zróżnicowanie tekstury czy ruch (Sáry, Vogels, Kovács i Orban, 1995), niezależnie od wielkości i położenia tych obiektów w polu widzenia (Ito, Tamura, Fujita i Tanaka, 1995; Logothetis, Pauls i Poggio 1995), a także niezależnie od tego czy są one widoczne w całości, czy też częściowo przysłonięte (Kovács, Vogels i Orban, 1995; Missal, Vogels i Orban, 1997).
Alan Slater i Victoria Morison (1985) oraz Alan Slater, Scott P. Johnson, Elizabeth Brown i Marion Badenoch (1996) badali zainteresowanie małych dzieci prezentowanymi kształtami różnych figur. Ustalili, że mechanizm odpowiedzialny za kodowanie złożonych kształtów, a w konsekwencji za stałość ich widzenia jest wrodzony. Już u kilkudniowych niemowląt stwierdzili oni habituację, czyli utratę zainteresowania znanymi kształtami oraz podwyższone zainteresowanie figurami, które miały nieznane im kształty.
Na drugim biegunie, w związku z procesami degeneracyjnymi starzejącego się mózgu może dojść do stopniowej dysfunkcjonalności tego mechanizm, co przejawia się pogłębiającymi się objawami agnozji kształtu, czyli niezdolności do trafnego rozpoznawania i odtwarzania widzianych rzeczy (Farah, 1990; Tippett, Blackwood i Farah, 2003). Zjawisko rozpadu kształtów widzianych rzeczy na tle zaburzeń neurodegeneracyjnych znakomicie odzwierciedlają autoportrety Williama Utermohlena (ryc. 140 A‑D).

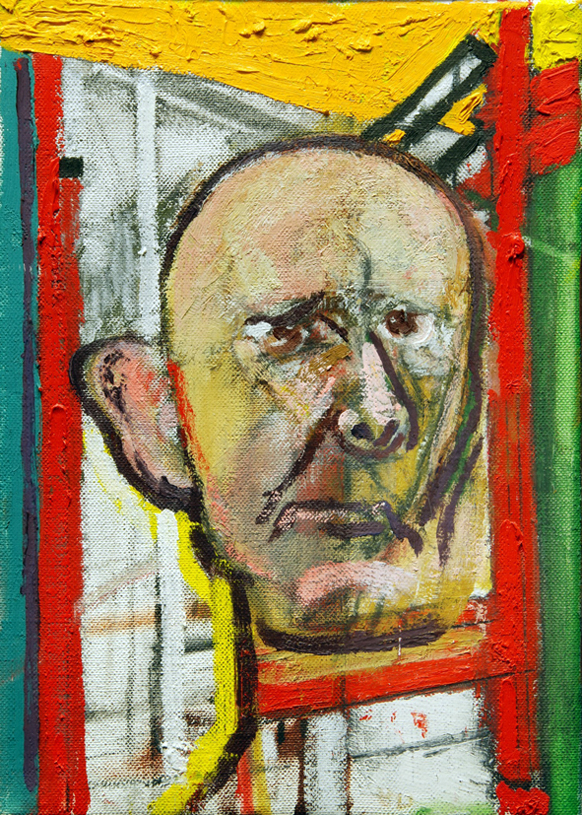


Z jednej strony, neuronauka dostarcza wielu przykładów malarzy, którzy tworzyli cierpiąc na migrenę, epilepsję, udar lub inne uszkodzenia mózgu, a także choroby neurodegeneracyjne. W roku 2006 cały zeszyt International Review of Neurobiology (tom 74) został poświęcony tej problematyce. Z drugiej jednak strony, sztuka współczesna aż kipi od przykładów świadomego, a nawet programowego łamania zasady stałości kształtu. Do klasyków w tej dziedzinie z pewnością należałoby zaliczyć malarzy kojarzonych z surrealizmem (ryc. 141), ekspresjonizmem (ryc. 142) i kubizmem (ryc. 143). Pomimo wielu różnic między nimi łączy ich traktowanie radykalnego odstępstwa od typowego kształtu rzeczy, jako środka wyrazu artystycznego.



Stałość wielkości (size constancy) jest zdolnością umysłu do trafnej oceny wielkości spostrzeganych rzeczy niezależnie od ich odległości od obserwatora, czyli innymi słowy bez względu na to jak duży obraz rzutują one na siatkówkę oka (Gibson, 1979; Kaufman i Kaufman, 2000; Konkle i Oliva 2011; Palmer, 1999). Stałość wielkości opiera się na wiedzy i doświadczeniu obserwatora, które podpowiadają mu, że spostrzegana wielkość znanych obiektów jest pochodną odległości, w jakiej znajdują się one od niego. Jest to tak oczywiste, że nawet nie zdajemy sobie sprawy z tego, jak ogromny jest wpływ dystansu w głąb na wielkość obrazów rzutowanych na siatkówkę oka przez obiekty znajdujące się bliżej i dalej od obserwatora.
Para młodych ludzi w prawym górnym rogu na ryc. 144 (strzałka A) znajduje się w odległości nie większej niż 15 metrów z tyłu za osobą z pierwszego planu, ale dopiero zbliżenie tych planów do siebie daje wyobrażenie o skali różnicy. Wysokość osób z drugiego planu nie przekracza 2/3 wysokości głowy osoby na pierwszym planie (por. ryc. 144, strzałka B). Pomimo tak dużej dysproporcji między wielkościami sfotografowanych ludzi bynajmniej nie mamy wrażenia, że osoby z drugiego planu są szczególnie niskie.

Poczucie stałości wielkości w zależności od dystansu w głąb jest jednak jeszcze bardziej niezwykłym doświadczeniem. Oto obraz Paolo Uccello, Sceny z życia świętych pustelników, na którym odległości między różnymi planami wynoszą, co najmniej kilkadziesiąt metrów (ryc. 145). W każdym z tych planów widzimy postaci, a ich wielkości akceptujemy równie łatwo, jak na ryc. 144. Różnica między tymi dwoma obrazami jest jednak zasadnicza. Postać klęczącego pustelnika widoczna z odległości 60–80 metrów w najdalszym planie stanowi około połowy wysokości największej postaci z pierwszego planu – pustelnika-wizjonera siedzącego w ławie z lewej strony. Gdyby sfotografować tę scenę w naturze wówczas klęczący pustelnik stałby się niewielkim punktem na horyzoncie. I wówczas, z pewnością także zaakceptowalibyśmy tę scenę, jako poprawnie odzwierciedlającą wielkości znajdujących się w niej osób i rzeczy. Jak to jest zatem z tą stałością wielkości na obrazach?

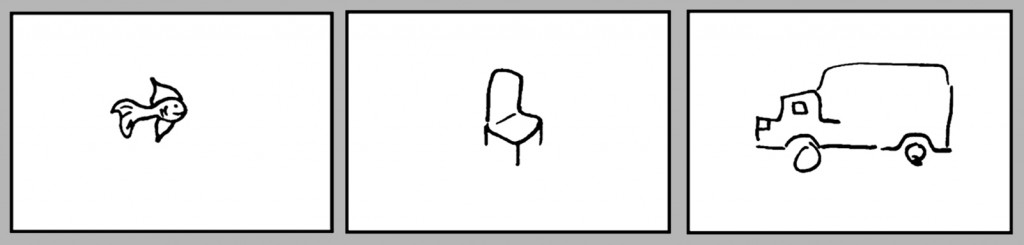
Dwa efekty stwierdzone przez Konkle i Olivę (2011) ujawniają specyfikę tej korekty. Pierwszy efekt dotyczy relatywizacji wielkości rysowanego przedmiotu do przestrzeni obrazu, wyznaczonej przez jego ramy. Okazuje się, że chociaż ryba, krzesło i ciężarówka, rysowane na trzech oddzielnych kartkach papieru o takich samych wymiarach zajmują, odpowiednio coraz większą powierzchnię, to przyrost wielkości nie jest prostoliniowy (jak byłoby w rzeczywistości), ale logarytmiczny (ryc. 146 A).
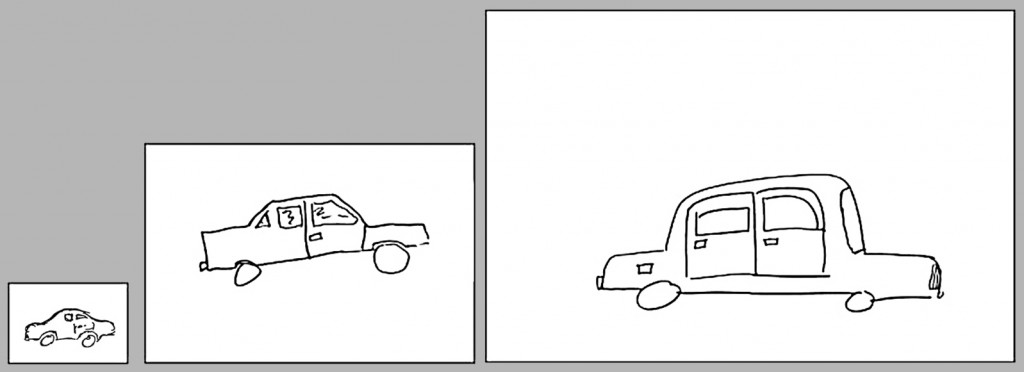
Drugi efekt stwierdzony przez Konkle i Olivę (2011) dotyczy relacji między wielkością powierzchni obrazu, wyznaczonej przez jego ramy, a wielkością rysunku tego samego obiektu. Proporcja wielkości samochodu na ryc. 146B do powierzchni kartki papieru, na której był rysowany jest mniej więcej taka sama, chociaż przyrost wielkości powierzchni obrazu do przyrostu wielkości rysowanego obiektu jest nieco większy z każdym następnym formatem papieru. Można zatem oczekiwać, że dla każdego obiektu przedstawionego na obrazie o określonej powierzchni istnieje pewna najbardziej preferowana (akceptowana) jego wielkość.
Żeby dobrze zrozumieć relacje wielkości obiektu przedstawionego na obrazie do wielkości jego powierzchni trzeba sobie jeszcze uświadomić, że rzeczywiste ramy obrazu, najczęściej zamkniętego w formę prostokąta, nie są jedynymi ramami odniesienia dla przedstawionych na nim obiektów. Na wielkość osób, zarówno na fotografii na ryc. 144, jak i na obrazie Uccello na ryc. 145 można spojrzeć nie tyle przez pryzmat widzenia przestrzeni w głąb, ile przez pryzmat wielu, w pewnym sensie, niezależnych od siebie planów, czy innymi słowy – obrazów w obrazie. Każdy z tych sub-obrazów ma swoją przestrzeń o określonej wielkości, w stosunku do której są relatywizowane wielkości znajdujących się w niej obiektów.
Niech jako przykład posłużą różne sceny z życia świętych pustelników, które wyjąłem z trzech różnych planów całego obrazu (ryc. 147). Okazuje się, że proporcje wielkości postaci do wielkości przestrzeni poszczególnych scen są mniej więcej takie same, niezależnie od tego, w którym planie są namalowane. Co więcej, w każdej z tych scen zachowana jest zasada stałości wielkości. Obiekty dalsze są relatywnie mniejsze niż bliższe.

Możliwości manipulacji relacją między stałością wielkości a wielkością kanoniczną stanowią przedmiot szczególnego zainteresowania niektórych wybitnych malarzy współczesnych. Chuck Close i Andy Warhol eksperymentowali z wielkością kanoniczną portretowanych twarzy na obrazach, przeskalowując je do wymiarów daleko odbiegających od typowych formatów zdjęcia lub odbitki kserograficznej. Nie tylko powierzchnia obrazu może przekraczać 10 m², ale również namalowana na niej twarz wypełnia ją niemal w całości. Nie bez znaczenia dla osiągnięcia pełni efektu artystycznego jest również to, że obrazy te są oglądane z niewielkiego dystansu w przestrzeni muzeum.




Wspomniane badania nad wpływem rozmycia obrazu na stałość kształtu i wielkości doprowadziły Hershel W. Leibowitza i Roberta B. Posta (1982) do twierdzenia, że o ile zbieraniem i utrzymywaniem informacji dotyczących kształtu zajmuje się system brzuszny (ventral pathway), odpowiedzialny za rozpoznanie przedmiotu (co wielokrotnie zostało już potwierdzone w innych badaniach), o tyle dane o wielkości obiektu są przetwarzane w systemie grzbietowym (dorsal pathway), zajmującym się jego lokalizacją, która stanowi podstawę do wykonania wobec niego czynności motorycznych. Do podobnych wniosków doszli kilka lat później Hide-aki Saito i współpracownicy (1986), którzy stwierdzili, że ok. 15% neuronów w okolicy skroniowej przyśrodkowej górnej (medial superior temporal area; MST), leżącej na szlaku grzbietowym jest wrażliwych na zmiany wielkości bodźca. Tym niemniej zagadnienie lokalizacji funkcji stałości wielkości jest znacznie mniej pewne, niż neuroanatomiczna lokalizacja funkcji stałości kształtu.
W wyniku badań prowadzonych nad pacjentką D.F., które doprowadziły Melvyna A. Goodale’a i A. Davida Milnera do uściślenia funkcji dwóch szlaków wzrokowych: brzusznego i grzbietowego, stwierdzono także, że pomimo braku uszkodzenia szlaku grzbietowego, pacjentka ujawniała problemy związane ze stałością wielkości, podczas wykonywania zadań pod kontrolą tylko jednego oka (Marotta, Behrmann i Goodale, 1997). Okazuje się, że uszkodzenie ośrodków odpowiedzialnych za rozpoznawanie złożonych kształtów rzeczy na szlaku brzusznym w połączeniu z widzeniem monoskopowym (jednoocznym) także powoduje trudności z prawidłową oceną ich wielkości.
Również Allan C. Dobbis, Richard M. Jeo, József Fiser i John M. Allman (1998) twierdzą, że za efekt stałości wielkości odpowiedzialne są zarówno struktury leżące na szlaku grzbietowym (MT), jak i brzusznym, wskazując zwłaszcza na obszar V4. Podsumowując, Helen Ross i Cornelis Plug (2002) uważają, że obecnie jest jeszcze zbyt mało danych, by można było z dużym prawdopodobieństwem wskazać na te struktury korowe, które są odpowiedzialne za stałość wielkości, a w każdym razie z pewnością nie należy oczekiwać, że leżą one wyłącznie na jednym z wymienionych szlaków wzrokowych.
Niezależnie od wcześniejszych ustaleń, wyniki najnowszych badań fMRI, przeprowadzonych przez Talia Konkle i Aude Olivę (2012) ujawniają, że małe obiekty, takie, jak np. moneta, fajka, liść lub kubek aktywizują neurony głównie w dolnej korze skroniowej (inferior temporal, IT) oraz w bocznej potylicznej (lateral occipital), natomiast duże obiekty, takie, jak np. fotel, komoda, wózek dziecięcy lub kosiarka – w przyśrodkowej górnej korze skroniowej (parahippocampal cortex) (ryc. 150). Oznacza to, że inne struktury mózgu reagują na dane dotyczące opozycji w zakresie wielkości widzianych obiektów podobnie, jak odmienne struktury mózgu przechowują dane i są odpowiedzialne za ich różnicowanie w odniesieniu do opozycji obiektów ożywionych (twarze i części ciała) i nieożywionych (Kriegeskorte, Mur, Ruff, Kiani i in., 2008), dotyczących twarzy i innych części ciała (Peelen i Downing, 2005) oraz odnoszących się do scen wizualnych i wyizolowanych z nich obiektów (Epstein i Kanwisher, 1998).
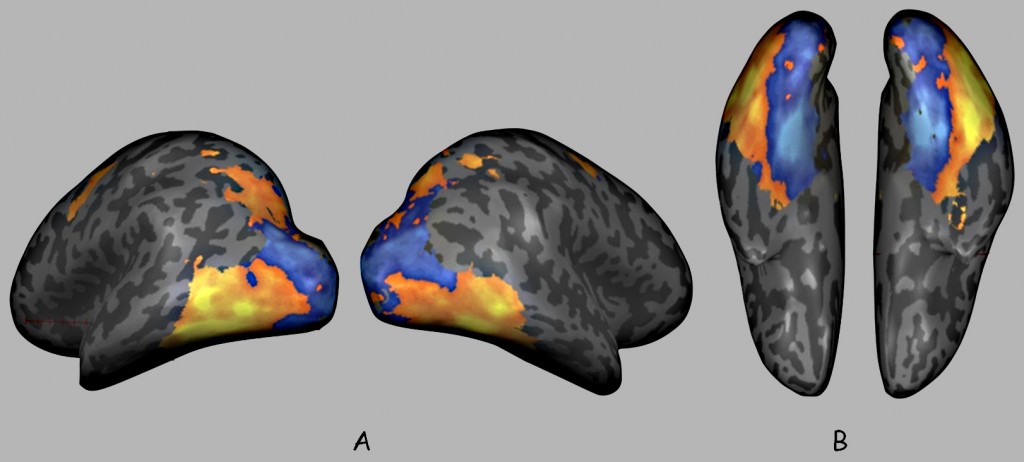
Interesującym wynikiem badań Talia Konkle i Aude Olivy (2012) jest również to, że aktywność wymienionych struktur mózgu jest niezależna od tego jak duży jest obraz siatkówkowy tych obiektów. Innymi słowy, niezależnie od tego czy ten sam obiekt rzutował na siatkówkę obraz o wielkości 4o czy 11o kąta pola widzenia, to aktywizował te same części kory skroniowej. Wyniki tych badań sugerują istotny związek między wiedzą o wielkości widzianych rzeczy a aktywizacją określonych struktur w korze skroniowej i potylicznej.
Łamanie zasady stałości wielkości jest jednym ze środków wykorzystywanych w sztukach wizualnych, które służą do podkreślenia ważności rzeczy lub osób. W starożytnym Egipcie, wielkość przestawianych postaci była interpretowana symbolicznie, jako oznaka ważności w hierarchii społecznej. Oto, na przykład, faraon Amenhotep IV (Echnaton), jego żona, królowa Nefertiti i córka, składają ofiarę bogu Atonowi (tarczy słonecznej) (ryc. 151 A). O wielkości postaci przedstawionych na papirusie bynajmniej nie decyduje ich odległość od obserwatora, ale ranga w państwie i rodzinie.

Niemal dokładnie ten sam wzorzec relacji ważności odzwierciedlony poprzez zróżnicowanie wielkości przedstawionych postaci można znaleźć w zachodnioeuropejskiej sztuce chrześcijańskiej (ryc. 151 B). Gdyby nie olbrzymi Archanioł Gabriel w środku sceny można by sądzić, że różnice w wielkości przedstawionych postaci Chrystusa i zmartwychwstańców są pochodną punktu widzenia obserwatora (z nieba w kierunku ziemi). Jednak przyjrzenie się rozmiarom osób z otoczenia Chrystusa także wskazuje na nieuzasadnioną warunkami fizycznymi dysproporcję w ich wielkości.

Wśród współczesnych obrazów także można znaleźć przykłady symbolicznego wykorzystania wielkości, jako wskazówki dotyczącej wagi przedstawionych obiektów, które łamią zasady stałości wielkości. Jednym z mistrzów takich anegdot jest bez wątpienia cytowany już René Magritte (ryc. 152).

INTERPOZYCJA
Najważniejszy wskaźnik głębi
Interpozycja (interposition) lub inaczej okluzja (occlusion) jest najbardziej oczywistym a zarazem najważniejszym wskaźnikiem głębi, zarówno w odniesieniu do sceny trójwymiarowej, jak i płaskiego obrazu, który ją przedstawia. Oznacza wzajemne przysłanianie się nietransparentnych obiektów, położonych w głąb oglądanej sceny wizualnej. Obiekt przysłonięty jest spostrzegany, jako znajdujący się dalej od obserwatora, niż obiekt, który go przysłania (ryc. 153 A). Pomimo oczywistości tego doświadczenia, bliższe przyjrzenie się mechanizmowi percepcyjnemu, który leży u jego podstaw ujawnia jego złożoność. Przede wszystkim, zanim system poznawczy obserwatora stwierdzi, który obiekt jest bliżej, a który dalej od niego, najpierw musi odpowiedzieć sobie na bardziej podstawowe pytanie: czy to, co właśnie widzi jest jednym obiektem w tej samej płaszczyźnie prostopadłej do osi widzenia, czy też wieloma obiektami, ustawionymi wzdłuż wymiaru w głąb.
Według Gaetano Kanizsy (1979) dla interpozycji charakterystyczne są skrzyżowania konturów: typu „L” i typu „T” (wewnątrz- i między-obiektowe). Kluczowe z punktu widzenia oddzielenia od siebie obiektów jest dostrzeganie między-obiektowych skrzyżowań typu „T”. Zjawisko interpozycji nie występuje w odniesieniu do obiektów transparentnych, czyli przeźroczystych (ryc. 153B). Typowym skrzyżowaniem konturów między obiektami transparentnymi są skrzyżowania typu „X”.
Zagadnienie interpozycji najczęściej rozważa się w dwóch kontekstach:
- gestaltowskich zasad spostrzegania figury i tła, które definiują relację między przesłaniającym i przysłanianym oraz
- percepcyjnej kompletności tego, co przysłonięte i poznawczej możliwości odtworzenia niewidzianej części.
Żeby zrozumieć, czym w istocie jest zjawisko interpozycji, trzeba najpierw przypomnieć sobie, w jaki sposób system wzrokowy rozpoznaje kształty pojedynczych rzeczy w scenie wizualnej. Podstawą widzenia każdego obiektu jest bowiem wyodrębnienie go z tła oraz oddzielenie od innych rzeczy znajdujących się w scenie na podstawie płaszczyzn i konturów, które je otaczają.
O ile jednak dobrze poznane są mechanizmy neuronalne pozwalające na identyfikację konturów, o tyle znacznie mniej wiemy na temat mechanizmów neuronalnych, które są odpowiedzialne za stwierdzenie, po której stronie konturu jest obiekt, a po której – tło.
Jeszcze w 1988 roku David Hubel, pisał: „Wiele osób, w tym ja, wciąż mają problemy z zaakceptowaniem idei, iż powierzchnia [leżąca między konturami widzianych rzeczy – P.F] nie jest w stanie pobudzić komórek nerwowych w naszym mózgu – że nasza świadomość wnętrza jako białego, czarnego lub kolorowego zależy tylko od komórek wrażliwych na krawędzie” (Hubel, 1988, s. 87). Trudność tę dostrzegali także teoretycy Gestalt i zaproponowali pojęcie granicy własnej obiektu (border ownership), która wskazuje na płaszczyznę należącą do figury, w odróżnieniu od płaszczyzny tła lub innych obiektów (Koffka, 1935).
Neuronalne podstawy interpozycji
Do dzisiaj nie jest znany mechanizm neuronalny odpowiedzialny za identyfikację płaszczyzny, jako leżącej po określonej stronie granicy własnej obiektu. Wyniki badań prowadzonych przez Hong Zhou, Howarda S. Friedmana i Rüdigera von der Heydta (2000) na małpach oraz Rüdigera von der Heydta, Toda Macudy i Fangtu Qiu (2005) na ludziach ujawniły jednak, że na wczesnych etapach korowego przetwarzania sygnałów wzrokowych, a dokładnie w obszarze V2, ponad 50% komórek w polu recepcyjnym, które biorą udział w kodowaniu konturu, intensywniej reaguje po wewnętrznej stronie prezentowanej figury, niż po zewnętrznej.
Philip O’Herron i Rüdiger von der Heydt (2009; 2011) pokazywali osobom badanym dwa rodzaje bodźców, przedstawionych na ryc. 154. Różnią się one stopniem zdefiniowania figury wewnątrz koła. Na planszy A znajduje się biały kwadrat, o wyraźnie odcinających się konturach od szarego tła koła. Na planszy B nie można natomiast zdefiniować, która część koła należy do figury, a która do tła. Owal leżący na styku płaszczyzn oznacza pole recepcyjne komórki zwojowej kodującej kontur. Barwa czerwona oznacza wysoką aktywność neuronów w polu recepcyjnym w obszarze V2, a niebieska – niską.
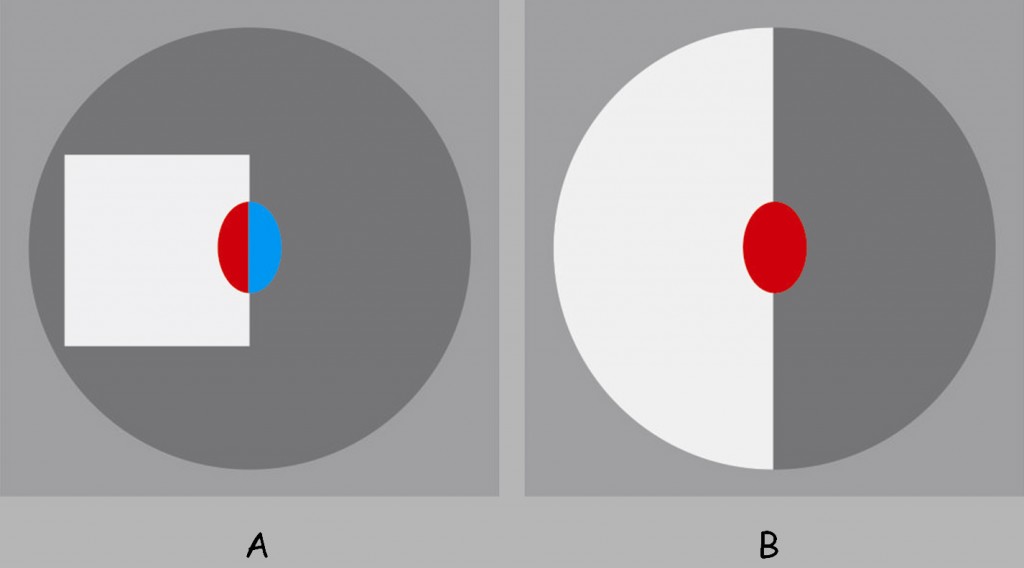
O’Herron i von der Heydt potwierdzili wyniki wcześniejszych badań, zgodnie z którymi komórki leżące w polu recepcyjnym po stronie figury były aktywniejsze (barwa czerwona) niż po stronie tła (barwa niebieska) (ryc. 154 A). Ustalili także, że intensywna aktywność komórek po obu stronach konturu w polu recepcyjnym w korze V2 utrzymuje się znacznie dłużej, nawet ponad jedną sekundę, wtedy gdy w bodźcu nie da się jednoznacznie wyodrębnić figury, tak jak na ryc. 154.B. Wyniki cytowanych badań świadczą o tym, że w korze V2 muszą istnieć wyspecjalizowane komórki, które identyfikując kontur rozpoznają, po której jego stronie jest figura, ale jak dotąd nie mamy pojęcia, co stanowi podstawę ich „wiedzy”.
Co łączy Strzemińskiego, rysowników z Chauvet i Leonarda da Vinci?
Interesującym przykładem artystycznej wariacji na temat przestrzeni sygnalizowanej konturami rozpoznawalnych rzeczy i barwnymi plamami są tempery Władysława Strzemińskiego (ryc. 155 A i B).


Przestrzenność sceny przedstawionej na obrazie można odczytać na kilka sposobów. Z jednej strony, niektóre domy zasłaniają się nawzajem (interpozycja), a inne są transparentne (obecne, ale pozbawione płaszczyzn). Niektóre z nich są zasygnalizowane tylko linią konturową, inne barwnymi plamami. Z drugiej strony, w obrazie można oddzielić od siebie warstwę swobodnej linii konturowej, która znajduje się przed warstwą barwnych plam. Linia ta bynajmniej nie należy jednak tylko do jednej płaszczyzny. Przeciwnie, obrysy okien są zdecydowanie bliżej, niż kominy na horyzoncie.
Jeszcze bardziej skomplikowana jest sytuacja na obrazie Bezrobotni (ryc. 155 A). Linie konturowe i barwne plamy przenikają się tutaj już zupełnie swobodne. Nie mamy jednak wątpliwości, że scena przedstawia grupę ludzi. Zastosowane przez Strzemińskiego środki podkreślają natomiast jej bezkształtność, nieistotność jednoznacznego porządku przesłaniania i ruchliwość, cechy tak charakterystyczne dla wyrażenia idei tłumu.
Z punktu widzenia zadania, jakie rozwiązuje system wzrokowy badając przestrzeń w głąb sceny wizualnej można doszukać się pewnej analogii między obrazami Strzemińskiego, a najstarszymi zachowanymi świadectwami aktywności malarskiej człowieka. Fotografia na ryc. 156 przedstawia fragment rysunków naskalnych z jaskini Chauvet. Najprawdopodobniej pochodzą one z ery paleolitu, sprzed ok. 30 tys. lat.

Oglądając te, jak i wiele innych rysunków naskalnych nie można jednoznacznie stwierdzić, w jakim stopniu kreślący je artyści świadomie stosowali zasadę interpozycji. Z jednej strony grupa zwierząt w górnej części ściany jest przedstawiona w taki sposób, że nie mamy wątpliwości, iż artysta wykorzystał interpozycję do przedstawienia uporządkowania kolejności zwierząt w głąb. Z drugiej strony, kontury dwóch grup zwierząt w dolnej części ściany przenikają się i nie mamy już takiej pewności czy przedstawiają one scenę trójwymiarową. Czy naskalne rysunki zwierząt nie przypominają efektów do jakich dochodził Strzemiński w swoich eksperymentach wizualnych? Być może jest to słaba analogia, ale niewykluczone, że naskalne rysunki, podobnie, jak unistyczne wariacje Strzemińskiego są przejawem doniosłych odkryć w dziedzinie przedstawiania na płaszczyźnie obrazu tego, co widziane.
Możliwa jest jeszcze inna interpretacja tych prehistorycznych dzieł sztuki. Te, jak i wiele innych rysunków naskalnych przypominają szkice, studium głowy lub ciała zwierzęcia, analogiczne do tych, jakie wypełniają szkicowniki niemal wszystkich artystów malarzy. Chociaż położenie głów zwierząt kreślonych przez Leonarda da Vinci i nieznanego artystę sprzed tysięcy lat mogą sugerować interpozycję, w istocie każdy z nich jest autonomiczny, a ich nagromadzenie obok siebie jest raczej motywowane oszczędnością miejsca, niż próbą odtworzenia wymiaru w głąb (ryc. 157 A i B). Rzecz w tym, że nie mamy pewności odnośnie do motywów powstawania rysunków naskalnych.


Jean Clottes i David Lewis-Williams (2009), David Lewis-Williams (2002) i Michael Winkelman (2002) twierdzą, że są one wyobrażonymi przedstawieniami (halucynacjami) obiektów szczególnego uwielbienia i respektu, którym ulegał artysta – najprawdopodobniej, szaman – w stanie transu. Z pewnością należały do nich duże zwierzęta, jak konie, bizony, nosorożce lub tygrysy. Motywy ich uwieczniania na ścianach jaskini mogły zatem mieć niewiele wspólnego z przedstawieniem rzeczywistości na obrazie, w tym znaczeniu, w jakim, np. Bernardo Belotto (Canaletto) malował Warszawę z różnych punktów widzenia. W każdym razie do dzisiaj ta zagadka nie doczekała się ostatecznego rozwiązania.
Rekonstruowanie niewidzianego według gestaltystów
Następnym ważnym zagadnieniem związanym z interpozycją jest odpowiedź na pytanie: w jaki sposób system wzrokowy interpretuje relacje między dwoma obiektami, których obraz siatkówkowy może sugerować, że jeden z nich zasłania drugi. Rekonstruowanie niewidzianego, Kanizsa (1979) nazywa amodalnym (amodal), podkreślając, że wiedza dotycząca tego, czego nie widać w obiekcie zasłoniętym nie może być zweryfikowana za pomocą żadnego ze zmysłów. Widzenie niekompletnych przedmiotów, zasłoniętych częściowo przez inne jest jednym z najczęstszych doświadczeń percepcyjnych i nie wydaje się, żeby ludziom sprawiało jakieś zasadnicze trudności rozpoznanie, który obiekt przysłania, a który jest przysłonięty, ani jak w całości wygląda obiekt przysłonięty. Trafne odtworzenie niewidocznych części zasłoniętego obiektu jest bowiem podstawą widzenia ich porządku w głąb.
Rozważając to zagadnienie, Rob van Lier, Peter van der Helm i Emanuel Leeuwenberg (1994) przeprowadzili interesującą analizę, weryfikującą trafność podstawowych zasad percepcji sformułowanych przez psychologów Gestalt. Jedną z nich jest zasada dobrej kontynuacji (good continuation), zgodnie z którą kształt zasłoniętej części figury jest zdefiniowany przez przedłużenie widocznych linii konturowych tej figury zgodnie z ich kierunkiem.
Warunkiem dobrej kontynuacji jest zatem lokalna analiza najbardziej prawdopodobnych miejsc styku dwóch figur zidentyfikowanych, np. na podstawie skrzyżowań typu „T”.
Widząc dwie figury znajdujące się po lewej stronie na ryc. 158 A, ludzie na ogół nie mają wątpliwości, że prostokąt przysłania kwadrat (rozwiązanie: b), a nie, styka się dwoma krawędziami z nieregularną figurą (rozwiązanie: a). Rozpatrując tę scenę w trzech wymiarach jesteśmy skłonni raczej uznać, że prostokąt znajduje się bliżej nas, niż kwadrat a nie, że prostokąt i nieregularna figura leżą w tej samej płaszczyźnie, stykając się ze sobą krawędziami.
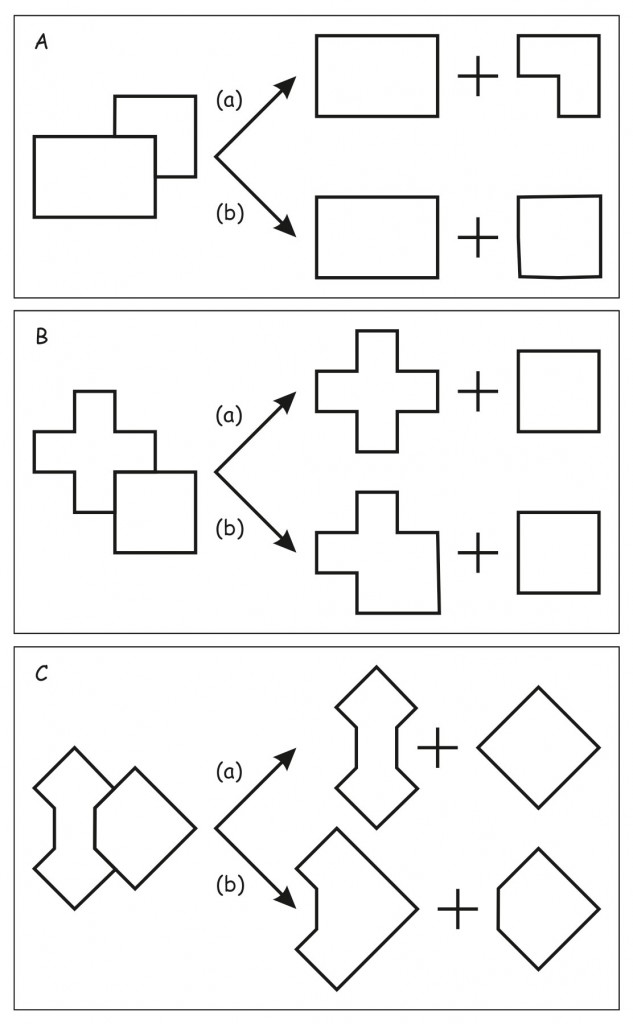
W przeciwieństwie do koncepcji akcentujących lokalną analizę miejsc styku przecinających się powierzchni dwóch figur, teoretycy Gestalt podkreślają także znaczenie globalnych zasad percepcji figur, takich jak prostota (similarity) i regularność (regularity), np. symetria (symmetry). Jako przykład realizacji tych zasad percepcyjnych w odkrywaniu zasłoniętej części jednej z figur, Rob van Lier i in (1994) prezentują ilustrację na ryc. 158 B. Okazuje się, że ludzie na ogół sądzą, iż widzą krzyż i kwadrat, które leżąc w tej samej płaszczyźnie stykają się ze sobą dwoma krawędziami (rozwiązanie: a) niż, że kwadrat przysłania nieregularną figurę (rozwiązanie: b). Warto zauważyć, że rozwiązanie (b) opiera się na zasadzie dobrej kontynuacji, a jednak o interpretacji tym razem decyduje prostota i symetryczność figury, która jest potencjalnie przysłonięta.
Okazuje się jednak, że zasad regularności i prostoty także nie można przyjąć, jako satysfakcjonującego wyjaśnienia przyjętej interpretacji, dotyczącej prawdopodobnego kształtu zakrytej części figury. Znakomicie ilustruje tę trudność trzeci przykład, na który powołują się Rob van Lier i współpracownicy (1994). Spoglądając na figury z lewej strony na ryc. 158 C, ludzie na ogół preferują rozwiązanie (b), które opiera się na zasadzie dobrej kontynuacji, niż rozwiązanie (a), odwołujące się do zasad prostoty i regularności. Okazuje się, że w tym przykładzie łatwiej jest dostrzec dwie mniej regularne i bardziej złożone figury, które leżą jedna na drugiej, niż leżące obok siebie dwie regularne i znacznie prostsze figury. Podsumowując, ani lokalne, ani globalne zasady percepcji figur sformułowane przez psychologów Gestalt nie mogą być uznane za wystarczające do wyjaśnienia decyzji dotyczących preferowanego kształtu zasłoniętej figury.
Percepcyjna złożoność vs złożoność pamięciowa interpretacji
Rob van Lier i współpracownicy (1994) zasugerowali, że być może rozwiązanie trudności kryje się w rozróżnieniu między percepcyjną złożonością (perceptual complexity) a złożonością pamięciową (memory complexity) interpretacji. Percepcyjna złożoność interpretacji odnosi się do procesu dochodzenia do preferowanego rozwiązania problemu relacji między figurami, natomiast złożoność pamięciowa interpretacji odnosi się wyłącznie do stanu końcowego, czyli właśnie do tego rozwiązania, które jest preferowane. Proces dochodzenia do ustalenia, czy dwie figury nakładają się na siebie oraz testowania zasad, które to rozwiązanie uzasadniają, może być bardziej lub mniej skomplikowany. Podobnie samo rozwiązanie może być bardziej lub mniej złożone, ale wiele wskazuje na to, że preferowane są przede wszystkim rozwiązania prostsze (bardziej ekonomiczne) niż skomplikowane, niezależnie od tego czy droga do nich opierała się na prostych czy złożonych zasadach (Hatfield i Epstein, 1985).
Van Lier ze współpracownikami (1994) skoncentrowali się głównie na analizie percepcyjnej złożoności. Tym niemniej z punktu widzenia problematyki interpozycji, rozumianej jako wskaźnik głębi, znacznie bardziej interesujące wydaje się zagadnienie pamięciowej złożoności interpretacji relacji między dwoma figurami.
Po pierwsze, jakkolwiek van Lier i in. (1994) wprowadzili to pojęcie, odróżniając je od pojęcia percepcyjnej złożoności, tym niemniej poprzestali tylko na jego ogólnej definicji. Pojęcie to nawiązuje do koncepcji Gary Hatfielda i Williama Epsteina (1985) oraz badań Freda Attneave’a (1954) nad relacjami między złożonością/prostotą a prawdopodobieństwem i redundancją, czyli powtarzalnością określonych wzorców percepcyjnych.
Złożoność/prostota pamięciowej interpretacji sceny wizualnej odzwierciedla prawdopodobieństwo lub powtarzalność określonego rozwiązania. Oznacza to, że preferowane rozwiązania relacji między figurami przedstawionymi na ryc. 158 są przejawem prostszej, to znaczy bardziej prawdopodobnej interpretacji pamięciowej, odwołującej się do wcześniejszych doświadczeń z podobnymi figurami. W tym kontekście warto skomentować preferencje rozwiązania (b) na ryc. 158C. Zamiast odwoływać się do wyników skomplikowanych analiz złożoności percepcyjnej obu figur i ich potencjalnych relacji wystarczy zwrócić uwagę na to, że prawdopodobieństwo sceny wizualnej, w której kształty dwóch figur doskonale pasują do siebie, jak w rozwiązaniu (a), jest znacznie mniejsze niż prawdopodobieństwo sceny, w której dwa bardziej skomplikowane kształty po prostu zasłaniają się nawzajem.
Po drugie, warto również zwrócić uwagę na to, że większość eksperymentów, których przedmiotem jest badanie przewidywania kształtów zasłoniętych części figur, opiera się na analizie figur dwuwymiarowych, czasem znanych, jak kwadrat, trójkąt czy koło, a czasem mniej znanych, wymyślonych wyłącznie na użytek badania. W naturalnych sytuacjach życiowych, a w szczególności oglądając obrazy, najczęściej mamy jednak do czynienia z obiektami znanymi (być może za wyjątkiem obrazów abstrakcyjnych). Oznacza to, że problem odtwarzania niewidocznych części obiektów należałoby rozpatrywać w kontekście pojęcia stałości kształtu. Na tej zasadzie obiekt częściowo przesłonięty nadal jest tym samym obiektem i można oczekiwać, że te części, które są dostępne wizualnie są wystarczające do wzbudzenia ich kompletnej reprezentacji w pamięci. Wsparciem dla tej hipotezy są wyniki badań, w których stwierdza się, że podczas oglądania obiektów częściowo przysłoniętych aktywizowane są dokładnie te same struktury mózgu na szlaku brzusznym, a zwłaszcza w okolicach zakrętu dolnego skroniowego (inferior temporal gyrus; IT), jak podczas ich oglądania w wersji kompletnej (zob. np. Kovács, Sáry, Köteles, Chadaide i in., 2003; Kovács, Vogels i Orban, 1995; Missal, Vogels i Orban, 1997).
Na pewno wiedział o tym Fidiasz, ale czy René Magritte – też?
Oglądając reliefy na fryzie Partenonu nie mamy żadnych wątpliwości, że rzeźbiąc je, Fidiasz dokładnie wiedział czym jest interpozycja i jak ją wykorzystać do przedstawienia iluzji w głąb na zdobionej płaskorzeźbą metopie (ryc. 159). Chociaż, za wyjątkiem pierwszoplanowych postaci, wszystkie pozostałe są tylko zasygnalizowane za pomocą większych lub mniejszych fragmentów, obraz jest w pełni zrozumiały i logiczny. Najprawdopodobniej wynika to stąd, że widoczne fragmenty są wystarczające do wzbudzenia ich kompletnych reprezentacji w pamięci obserwatorów. Interpozycja, jawi się zatem jako wynik rozbieżności między kompletną reprezentacją obiektu wzbudzoną w pamięci na podstawie jej części, a niekompletnym jej obrazem rzutowanym na siatkówkę oka. Ten układ jest interpretowany przez system, percepcyjny, jako wskaźnik głębi.
Przedstawianie wymiaru w głąb na płaskiej powierzchni obrazu za pomocą interpozycji jest jedną z najbardziej oczywistych i najczęściej stosowanych technik w sztukach wizualnych.

Dla współczesnych malarzy interpozycja stanowi jednak również pretekst do eksperymentowania. René Magritte namalował amazonkę, łamiąc regułę interpozycji i czyniąc z niej odrealnioną zjawę ze świata marzeń sennych (ryc. 160). Amazonka przenika trzeci wymiar w taki sposób, jak igła niedbałej szwaczki przeszywa kanwę, niezależnie od porządku wertykalnie ułożonych nici. W rezultacie niektóre z nich ulegają nienaturalnym zagięciom. I chociaż nie jest to zasadnicza przeszkoda w poprawnym odczytaniu obrazu, tym niemniej takie przedstawienie sceny wizualnej zmusza odbiorcę do refleksji na temat natury przestrzeni, a zwłaszcza jej wymiaru w głąb.

